Le relevé d’architecture
Un projet en questions, sous le regard de Villard de Honnecourt par Patrick Thépot
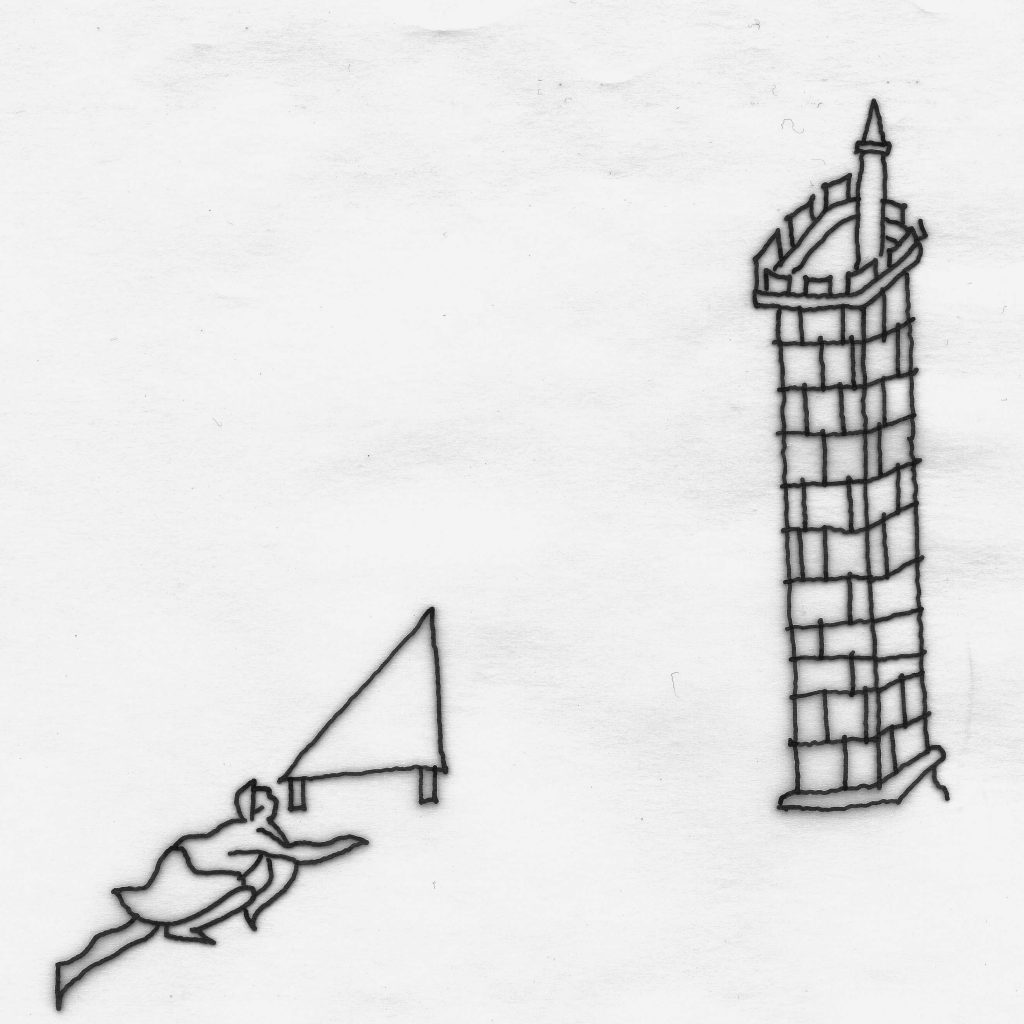
Relever est un acte simple. La succession des opérations qui s’y déploient nous entraîne toutefois dans un monde où abstrait et concret se confondent. Ce monde où la géométrie, inventée dit-on pour mesurer le sol afin qu’il soit chaque année, après chaque crue du Nil, de nouveau transformé en terre nourricière, permet aussi la construction en hauteur des plus grands édifices comme nous le montre l’architecte Villard de Honnecourt dans ses carnets du XIIIe siècle. Une équerre de visée, un fil à plomb, une canne de mesure sont les outils du relevé pour le chantier. Ils créent aussi l’espace mental du projet d’architecture. Pour illustrer notre propos, par le biais d’un redessin, le releveur agenouillé et la tour qu’il va mesurer sont extraits d’un des folios du carnet de l’architecte médiéval. Nous pouvons ainsi nous poser cette question : de quelle façon un relevé est-il mis en œuvre? Nous entrons alors de plain-pied dans l’espace de la fabrication du relevé en laissant volontairement aux savants spécialistes de l’architecture du Moyen-âge la partie supérieure du folio1. Cette interrogation nous projette d’abord face à l’édifice à relever alors que rien n’existe encore sinon l’édifice lui-même, situé dans son contexte en une spatialité qui nous englobe. Tout reste à faire avant d’obtenir cette finalité dessinée qui deviendra le début d’un accomplissement à interpréter. Un univers tridimensionnel s’inspirant du réel est donc à construire dans une totalité virtuelle par des allers/retours permanents entre le monde sensible et celui de l’intelligible. Cette approche physique/métaphysique convoque les actes essentiels que sont la mesure, le report et le tracé.
Au premier regard, dans l’alliance subtile de l’écrit et du dessin de la partie basse du folio, le petit personnage agenouillé semble être l’acteur principal [B. L’architecture représentée pourrait n’être que décor ou simple mise en scène. Si nous observons plus attentivement les édifications proposées, elles racontent en fait plusieurs actions spécifiques qui nous confrontent à une trilogie dont l’ordre de lecture nous invite à une chronologie des opérations mises en œuvre dans l’acte du relevé. Par subdivision en blocs séparés, les textes inscrits se décomposent en trois temps et viennent en aide au lecteur pour identifier un ordre d’interventions parfaitement distinctes. De ces inscriptions en vieux français, nous ne garderons que la traduction. Elles sont à considérer comme des instructions riches d’enseignement indissociables des dessins qui leur correspondent. C’est ce que nous allons tenter d’examiner.
“De cette façon on prend la hauteur d’une tour2” ou la question de la prise de mesure
Dans l’action de déterminer la valeur de dimensions, la prise de mesure coïncide avec un déplacement immatériel. L’intervention réclame un aller et un retour que nous devons imaginer suivant un trajet triangulé qui emprunte aux sources de la géométrie et aux enseignements de notre jeunesse conjugués: le théorème de Thalès. D’un point fixe qui nous représente, nous formulons une demande à un autre point qui, lui, est éloigné. La distance qui les sépare devient l’intervalle à interpréter en une restitution qui est la mesure attendue. De ce va-et-vient naît l’espacement dans l’écart qui nous divise de l’objet mesuré. L’ensemble s’inscrit dans une épure, c’est-à-dire un plan qui se soumet aux lois de la géométrie par le biais de triangles. Au paragraphe “de la pyramide au tétraèdre: origine optique3”, Michel Serres décrit deux légendes liées à la géométrie d’un fond commun homothétique. Elles sont celles de Diogène Laërce et Plutarque qui mêlent pyramide, soleil et ombre dans l’observation critique d’une histoire d’angles. Il s’agit de mesurer légitimement la hauteur d’un édifice inaccessible dont l’ombre portée devient le passage à l’accessible par la projection du sommet au sol. En un schéma réduit qui fait appel à la science mathématique, le modèle donne naissance au module. L’échelle change mais l’angle est conservé. Dans cette opération, il est important de noter que les triangles sont d’abord rectangles avant d’être semblables. Pythagore avant Thalès. Leurs rapports nous transportent de l’intangible au tangible. L’opposition initiale réside entre ce que l’on peut voir et ce que l’on peut toucher. “La vue est un tact sans contact4”, nous voyons le point culminant inaccessible et pourtant nous ne pouvons le toucher. Dans cet échange d’interceptions, par réduction, la mesure résulte de la hauteur recherchée. Le concept des triangles semblables emprunté au théorème de Thalès permet de nous situer dans l’espace en un voyage qui conduit à la mesure. Ainsi, la philosophie du fondateur de l’école de Milet anime le petit releveur agenouillé de Villard de Honnecourt pour nous rappeler toute l’importance d’une prise de mesure et la tour crénelée en est le prétexte.
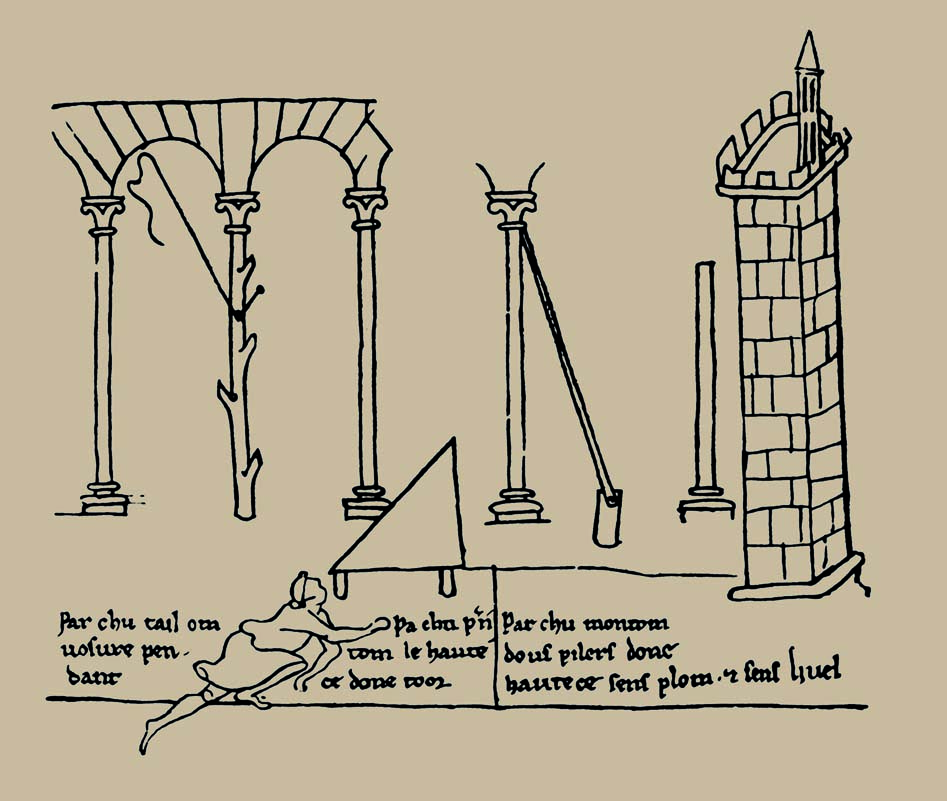
Détail de la partie inférieure du folio 20v – planche 40. Docci Mario, Maestri Diego, Storia del rilevamento architettonico e urbano, Editori Laterza, 1993, p. 55
“C’est ainsi que l’on monte deux piliers d’une (même) hauteur sans plomb et sans niveau5” ou la question du report
Le report de la mesure est une transposition qui participe aussi d’un voyage cependant dissemblable du précédent. Le même devient autre tout en étant le report de l’origine. Une mesure identique à la source se trouve transportée pour être répétée. Par ce transfert, Villard de Honnecourt nous entraîne dans les techniques de chantier qui seront poursuivies par Brunelleschi à la Renaissance. Avant qu’il conçoive le célèbre dôme de Santa Maria del Fiore, l’architecte florentin réalise pour Santo Jacopo sopr’Arno une première coupole a creste e vele6 construite sans cintres et sans échafaudages partant du sol. Ce procédé sollicitait l’usage d’une canne tournant sur elle-même pour assurer le report des mesures et anticipait, en réduction, l’ingéniosité de la grande coupole proposée pour la cathédrale toscane. L’ingenium7 et l’inventio8 de l’ami Alberti sont à l’œuvre pour nous faire réfléchir sur tout transfert.
En s’affranchissant du niveau indispensable à l’équilibre d’une construction par la perpendiculaire, Villard de Honnecourt nous permet de supposer que la colonne qui sert de modèle et celle qui reste à édifier sont déjà toutes deux dressées à la verticale. Entre les deux colonnes, un pivot articule une canne de mesure pour nous orienter du fini, qui sert de référence, au non fini en attente d’une arase. Et nous pouvons évoquer cet acte autant dans l’espace d’une construction en cours que sur une feuille de papier lorsque le report de la mesure met en lien les points qui préfigurent l’édifice, par plans orthogonaux, en attente d’une existence à lire à plat.

Manuscrit, folio 20v – planche 40. Bechmann Roland, Villard de Honnecourt, la pensée technique du XIIIe et sa communication, Paris, Picard, 1991, p. 140
“De cette façon on taille une voussure pendante9” ou la question du tracé
Le tracé synthétise les mesures relevées et désormais reportées en reliant point par point chaque partie du corps arpenté. Le chemin suivi révèle progressivement l’édifice par des lignes a priori abstraites. Cette abstraction est nécessaire et devient la condition indispensable pour projeter les points mesurés en langage qui est celui du dessin. “Par une volonté condensée, nous transformons le grand monde en petit monde. Il est mis à plat avec suffisamment d’imagination pour prévoir ainsi tout ce qui sera nécessaire lors de la transformation de nos notes jusqu’au résultat final10”. Le problème du choix de l’échelle se pose et Villard de Honnecourt nous offre le tracé constructif d’une voussure à l’échelle grandeur nature [E. Une corde partant d’un point fixe centré entre les deux arcs devient le lien qui vérifie les angles de la trompe de la voussure pendante. Dans la pratique, pour tendre la corde, l’opération devait s’effectuer au sol, donc sur un plan horizontal. Villard de Honnecourt, qui avait forcément une compréhension exemplaire de la taille des pierres, et donc du tracé au sol en correspondance avec la verticale à construire, nous ramène l’horizontale à la verticale. Entre grave et léger, par rabattement, se dessinent, en ce qui sera nommé des siècles plus tard géométrie descriptive, toutes les séparations linéaires qui procurent l’assemblage des éléments constructifs. La géométrie revient au premier plan pour répondre à tout tracé indispensable à la réalisation de l’œuvre.
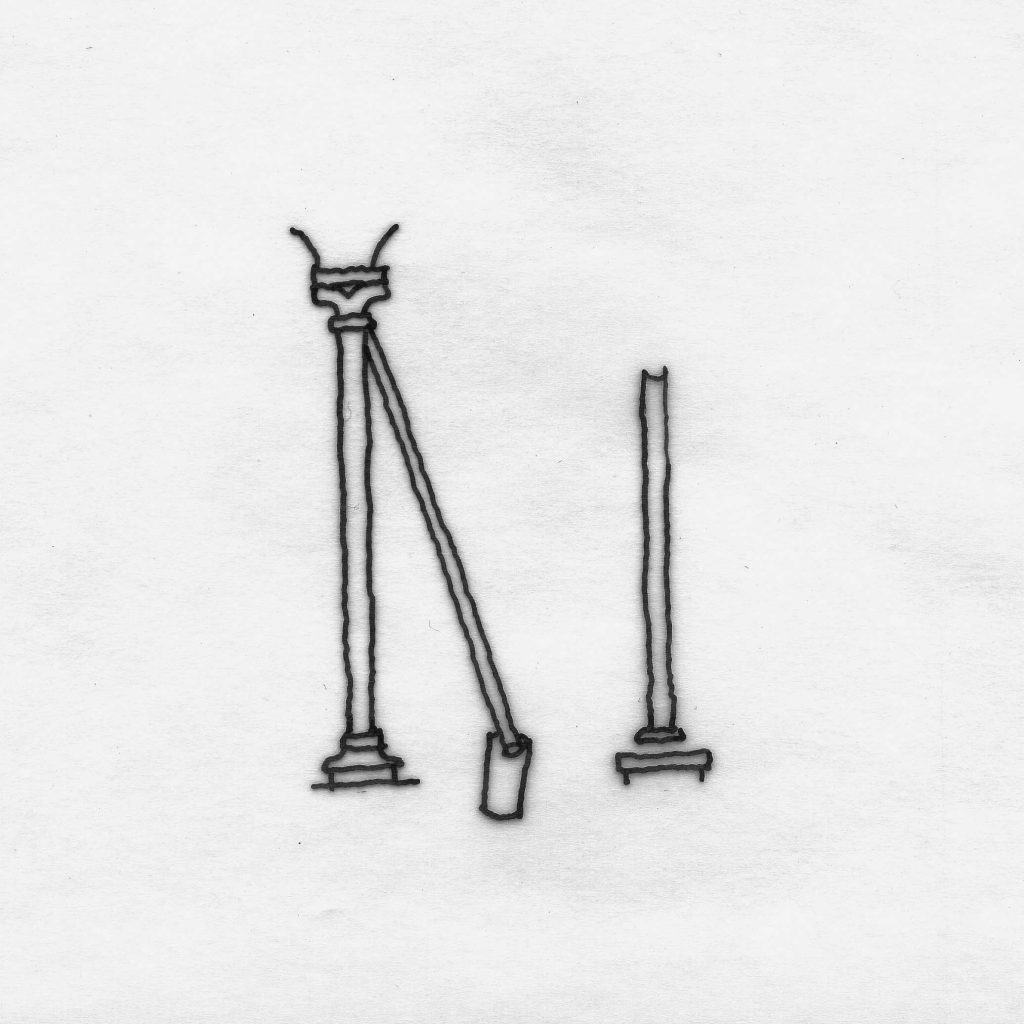
Le report de la mesure pour l’arase en attente. Thépot Patrick, dessins à l’encre de chine sur calque
De la pensée assemblée aux actions pratiques
En regardant plus précisément cette partie inférieure du folio, tout ce qui est dessiné à plat, c’est-à-dire sans relief ou sans épaisseur, nous plonge dans le monde intérieur de la pensée qui renferme l’abstraction [B. Le triangle du releveur, les deux piliers dont l’un est en attente d’une arase et la voussure pendante sont des outils de pensée avant d’établir le rapport indispensable à la mesure et ses prolongements. Par une opération mentale, ces outils nous font sortir du folio sans nous isoler complètement de la réalité afin de parvenir à connaître les propriétés de ce qui nous entoure. Cette recherche par la connaissance entretient un premier apport d’un rapport nouveau.
D’une autre façon, tout ce qui est montré en perspective dite naturalis11 ou en relief, nous projette en profondeur dans le monde extérieur des actions pratiques. Ce passage du dedans au dehors est à considérer tel un échange où réside une transaction. Ce pacte nous permet de reconsidérer le relevé comme une traduction de l’espace édifié qui passe par une représentation dessinée via la mesure. Et nous pouvons dissocier l’acte de la prise de mesures des dimensions reportées. Voir, toucher ou entrer en contact avec la réalité physique sont des expériences de la connaissance. La prise de mesures nous oblige à nous situer dans l’espace et les dimensions arpentées donnent les rapports qui existent entre l’édifice et ses parties dont l’ensemble s’inscrit dans le lieu.
Pour ce qui apparaît semblable à du relief, nous avons en entrée le petit releveur agenouillé qui trouve son équilibre en croisant les bras. Sa tête se redresse pour mieux pointer le faîte de la tour et si nous ne voyons l’œil qui vise le sommet, nous en comprenons la trajectoire grâce à l’hypoténuse du triangle qui donne la direction à suivre. Et la tour elle-même, d’un appareillage sommaire, donne à lire un petit clocher en terminaison. Il est l’inaccessible qui devient accessible pour relier le ciel et la terre. Et à une échelle plus réduite, le sommet et le sol s’ajustent par la mesure. Quant au fil à plomb et au niveau, dont il nous est proposé de nous affranchir, ils supposent une perpendiculaire préexistante dont Villard de Honnecourt garde le secret. Toute l’attention semble portée sur le pivot légèrement décalé par rapport à l’horizontale organisant la base des deux piliers. Comme pour lui octroyer une indépendance dans la manœuvre, ce cylindrique devient l’appui indispensable qui articule la canne dans l’espace devenant l’objet de l’ingénieux transfert. La colonne primitive située entre les deux arcs jumelés pourrait s’apparenter à celle moins rustique et d’un ordre codifié par Philibert de l’Orme12. Elle nous rappelle l’origine de l’architecture qui avant d’être de pierre était de bois ainsi que l’histoire de l’architecture de Choisy le décrit encore au XIXe siècle13. Le choix de ce pilier de substitution ne va pas si loin, sa représentation mal dégrossie n’est là que pour montrer qu’il est condamné à disparaître après avoir rempli son rôle. Sa participation éphémère permet le départ de la corde qui ne demande qu’à se tendre pour rayonner depuis un clou plutôt affirmé.
Toutes ces opérations inscrites dans le bas du folio en provenance des actions mesurées du monde extérieur sont inséparables de la connaissance pour mener à bien un relevé d’architecture. Et si les trois temps dissociés de ces processus respectent un ordre hiérarchisé pour obtenir une finalité dessinée, nous ne pouvons oublier que ces élaborations deviennent le début d’autre chose afin d’orienter et de continuer une pensée qui ne demande qu’à s’ouvrir pour déployer de nouvelles hypothèses et sont le propos du projet d’architecture.
- Bechmann Roland, Villard de Honnecourt, la pensée technique du XIIIe et sa communication, Paris, Picard, 1991, pp. 219-224. L’auteur relate avec une infinie précision comment le document est passé sous un éclairage ultra-violet et sous une lumière à infra-rouge en une confrontation avec différentes thèses explicatives.
- “(P)ar chu prent om le hautece done toor est traduit par de cette façon on prend la hauteur d’une tour” in Bechmann Roland, ibid., p. 156.
- Serres Michel, Les origines de la géométrie, Paris, Flammarion, 2004, p. 195
- ibid., p. 194
- “(P)ar chu mont om dous piliers done hautece sens plom et sens nivel est traduit par c’est ainsi que l’on monte deux piliers d’une (même) hauteur sans plomb et sans niveau” in Bechmann Roland, Villard de Honnecourt, op. cit., p. 148. Il est à noter que le terme colonne n’est pas utilisé mais le terme pilier. Nous conservons néanmoins colonne pour ce texte.
- Argan Giulio Carlo, Brunelleschi, Paris, Macula, 1981, p.154. (Dans son ouvrage cité en référence, Roland Bechmann décrit précisément le système de perche sur pivot utilisé par Brunelleschi, p. 150)
- Alberti Leon Battista, La peinture, (texte latin, traduction française, version italienne, éd. de Thomas Golsenne et Bertrand Prévost revue par Yves Hersan)t, Paris, Seuil, 2004, p. 340
- ibid., p. 349
- “Par chu tail om vosure pendant traduit par de cette façon on taille une voussure pendante” in Bechmann Roland, Villard de Honnecourt, op. cit., p. 195
- Thépot Patrick, “Relever c’est révéler le site”, in Queysanne Bruno, L’architecture inquiétée par l’œuvre d’art, Montpellier, éd. de l’Espérou, 2015, p. 129
- Damisch Hubert, L’origine de la perspective, Paris, Flammarion, 1987, p. 7
- Summerson John, Le langage de l’architecture classique, Paris, L’Equerre, 1981, p. 98
- Choisy Auguste, Histoire de l’architecture, tome I, Genève-Paris, Saltkine Reprints, 1987 (réimpression de l’édition de Paris, 1899), p. 3